Understanding Partial Order Alignment for Multiple Sequence Alignment

Jared’s nanopolish tool for Nanopore data uses poaV2, the original partial order alignment software described in papers by Lee, Grasso, and Sharlow ^1,2,3, for correcting the reads, following a similar approach taken by PacBio in PBDagCon.

This post gives a quick lower-level overview of the steps in the POA algorithm, with a simple implementation in python to demonstrate the ideas more concretely.

The Basics

The insight of the first POA paper was that “flattening” of the alignment of sequences leads to meaningless artifacts that, while largely harmless for pairwise alignments or even multiple alignments of strongly conserved sequences, causes problems with more general multiple alignments. For instance, consider the following sequences:

>seq1
CCGCTTTTCCGC
>seq2
CCGCAAAACCGC

There is ambiguity in selecting a single, best alignment between this pair of sequences; for instance below are 4 of

2⁸ = 256

8 choose 4 = 105 nearly equivalent ways of expressing this pairwise alignment. The best alignment will depend on the particular gap-scoring scheme used.

CCGC----TTTTCGCG   CCGCTTTT----CCGC  CCGC-TT-TT--CGCG   CCGC-T-T-T-TCCGC
CCGCAAAA----CGCG   CCGC----AAAACCGC  CCGCA--A--AACCGC   CCGCA-A-A-A-CCGC

While for a pairwise alignment this is comparatively harmless, as additional sequences are added to form a multiple sequence alignment (MSA), the choice between these ambiguities begin to distort the eventual result. What we would like is to consider not necessarily a single linear layout, but something that can express more unambiguously “one sequence inserts a run of A, and the other of T”. And a natural way to view that is with a graph:

The partial order alignment graph differs from the alignment strings in that a given base can have multiple predecessors (eg, the C after the fork being preceeded by both a string of As and of Ts) or successors (eg, the C before the fork). But it is similar to the alignment strings in that there is a directional order imposed, both in the sense that each node has (zero or more) predecessors and (zero or more) successors, but also that no repetition, or doubling back, is allowed; the graph is constrained to be a Directed, Acyclic Graph (DAG).

Both repeats and re-orderings can be biologically relevant, and various generalizations of alignment have allowed this ^4,5. This greatly generalizes the problem, moving it closer to assembly. For the purposes of error correction in nanopolish, that additional generalization is not needed.

Smith-Waterman

To consider how alignment to a graph works, let ’s remind ourselves of how we perform alignment on sequences.

In the Needleman-Wunsch algorithm and its variants, we consider two cursors - one on a base in each sequence. For each pair of cursor positions in turn, we consider the question of “what is the best sequence of alignments and insertions that could lead to this position in the alignment”. Because the globally optimal path must be made from locally optimal “moves” (that is, the “principle of optimality” holds for this problem), this reduces to finding out which of the three possible moves that would advance the cursors to this position to choose from:

• Both cursors having advanced, aligning (matching) these two bases;
• Cursor 1 had advanced while cursor 2 remained fixed, inserting that base from sequence 1 into the alignment
• Vice versa, with cursor 2 advancing and cursor 1 staying fixed.

A familiar diagram follows below; of those three possible moves, we take the running scores from each of those previous positions, add the score corresponding to the move, and set the score of the current position.

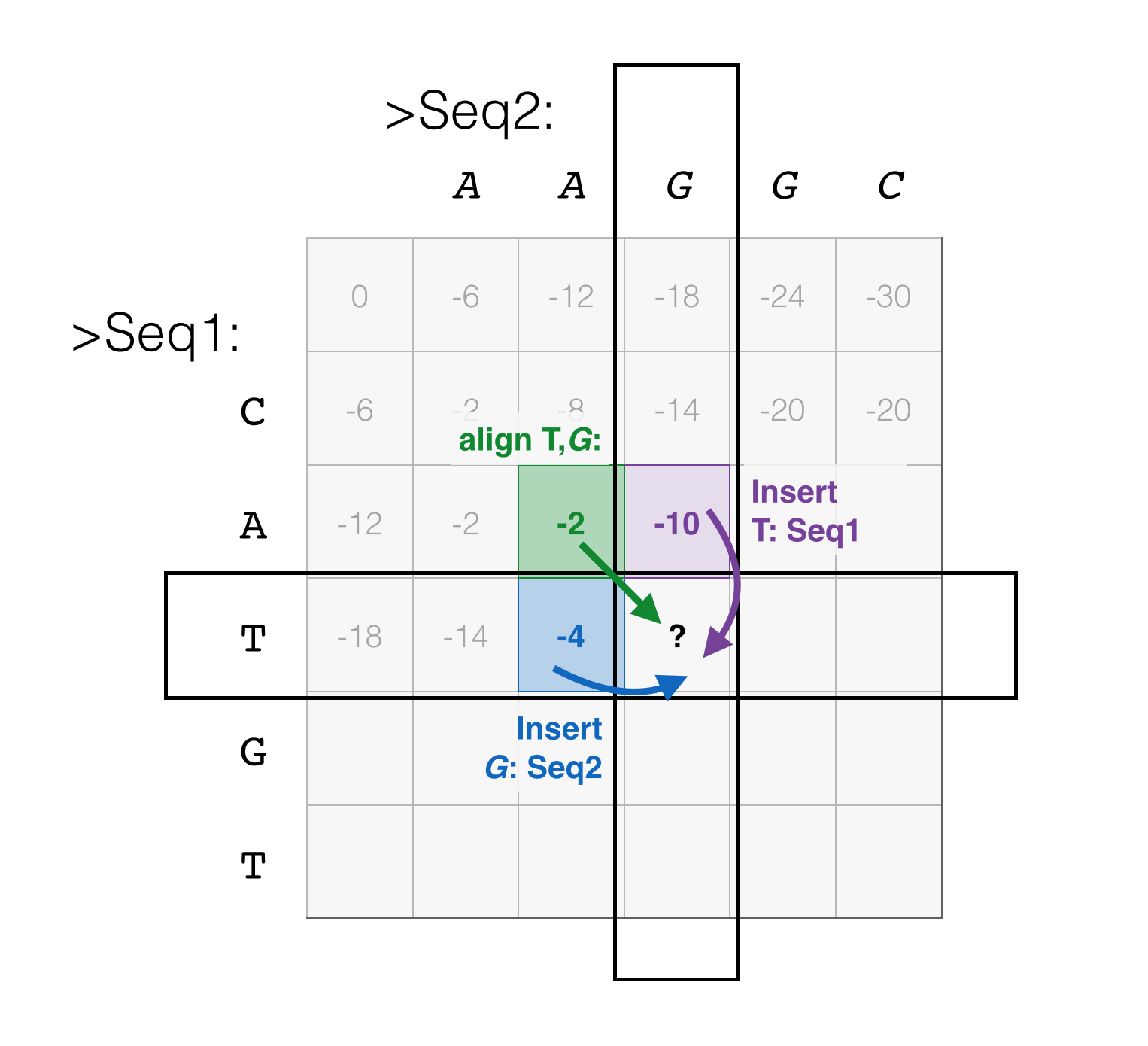
We can calculate the scores for pairs of positions in any order we like – along rows of the matrix, columns, or minor diagonals – as long as for any position we calculate, the scores for the previous positions we need have already been calculated.

String to Graph Alignment

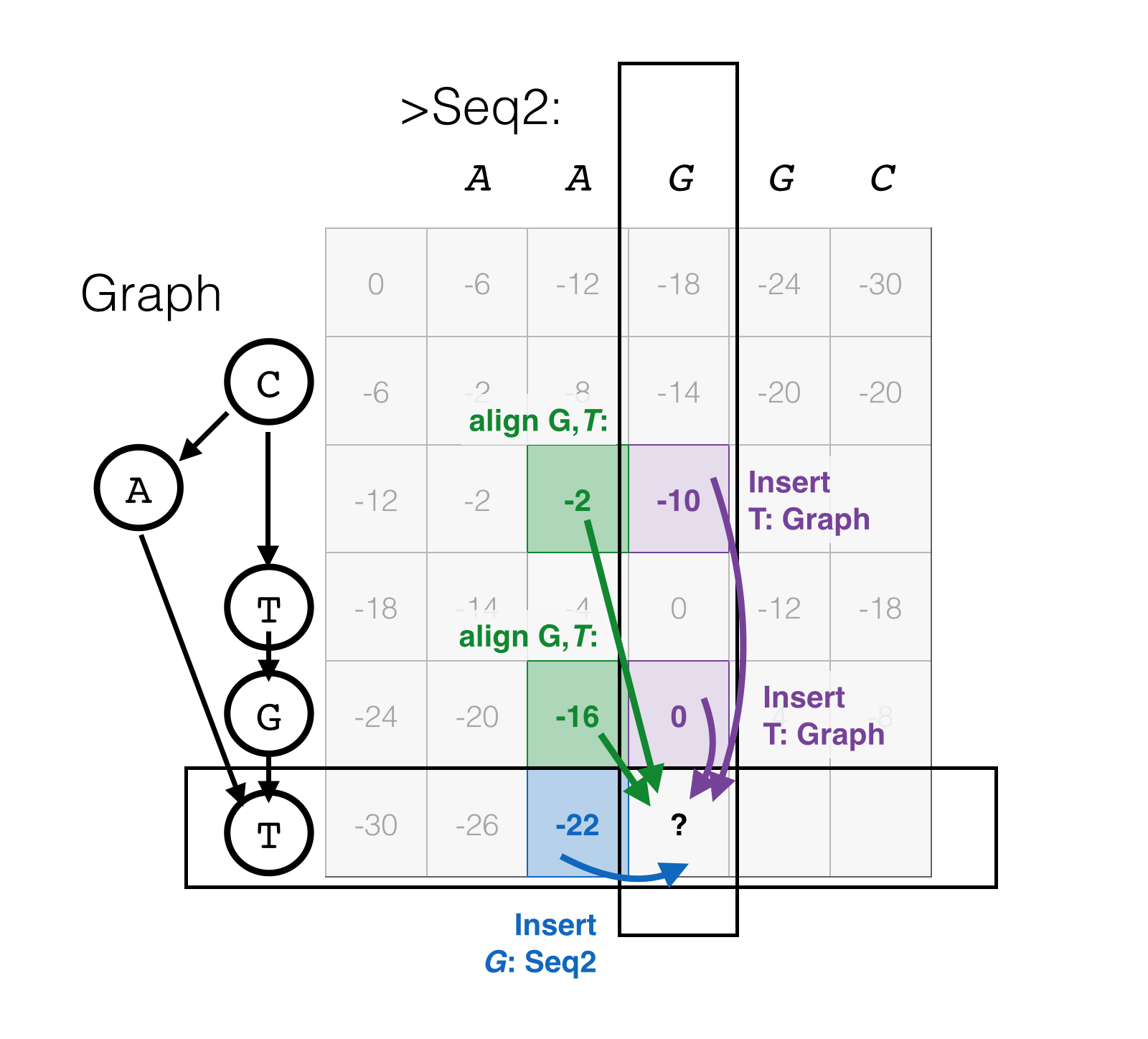
Aligning a sequence to a DAG introduces suprisingly little complexity to the dynamic programming problem; the clever diagram in the POA paper with a dynamic programming matrix with 3D “bumps” may have had the unintended consequence of making it look more complicated than it is.

The primary difference for the purposes of dynamic programming is that while a base in a sequence has exactly one predecessor, a base in a graph can have two or more. Thus, the cursor may have come from one of several previous locations for the same (graph) Insert or Align moves being considered; and thus those scores must be considered too in determining the best previous position. (Note that insertions from the sequence are unchanged).

So, to reiterate: the only difference deep inside the dynamic programming loop is that multiple previous scores (and any associated gap-open information) must be considered for insertions or alignments of the graph base. This is implemented by a loop over predecessors for the current base, and all else remains the same.

Topological Sort

There is one step that has to happen before that dynamic programming loop, however.

When aligning two sequences, one could choose an order to loop over the sequence indices before hand so that, for any new position being calculated, the necessary previous scores would already be ready.

The nodes in the graph, however, do not have such a useful intrinsic order. If the nodes are considered in the order they are added, for instance, then the newest nodes inserted with a new sequence – which may have been inserted as predecessors of nodes that had been inserted earlier – will not have been already scored when their successor begins its calculation.

The answer is to use a Topological Sort to generate an ordering of nodes in which every node is guaranteed to follow all of its predecessors. This is always possible for a directed graph as long as there are no cycles, and indeed there can be many such orderings. Topological sorts are how make and similar tools decide in which order to perform tasks in a workflow, and how many⁶ spreadsheet programs decide if cells need to be updated.

There are two main classes of algorithms for performing topological sorts; the algorithm of Kahn (1962), and a repeated depth-first search. Either serves perfectly well for the dynamic programming problem.

So to align a sequence to a graph, the steps are simply:

• Perform a topological sort if the graph has been updated
• Do the dynamic programming step as usual, with:
  • The graph nodes visited in the order of the topological sort, and
  • Considering all valid predecessors for align/insert moves.

Insertion of aligned sequence

Consider that we have a graph that so far only contains the sequence CGCTTAT, and our dynamic programming calculation aligning the sequence CGATTACG has given us an alignment that looks like this:

CGATTACG
||.|||.
CGCTTAT-

That is, for each base in the sequence, it is paired (either as match or mismatch) with a base in the graph, or it is inserted.

We expect inserting the new sequence into the graph to give us something like:

Here we see for the first time two types of edges; bold, directed edges (with directions not shown, but left-to-right), indicating predecessor/successor; and dashed lines, indicating that (say) the A and C that are three bases from the start are aligned to each other, but are mismatches; similarly with the C and T towards the end.

We keep track of both the predecessor/successor nodes and all ‘aligned-to’ nodes. We walk along the sequence we are inserting and its calculated alignment. We insert nodes in the sequence if they are not aligned to anything, or none of the nodes that it directly or indirectly aligns to have the same base; otherwise, we re-use that node and simply add new edges to it if necessary.

In more detail, the steps we take are as follows:

• A new “starting point” for this sequence is created in the graph.
• The previous position is set to this starting point.
• For each sequence base in the calculated alignment,
  • If the current base is not aligned to a node in the graph, or if it is but neither the node nor any node it is aligned to has the same base,
    • A new node is created with the sequence base, and is selected as the current node
    • This new node is aligned to the aligned node if any, and all of the “aligned-to” nodes are updated to align to this one.
  • Otherwise,
    • That node with the same base is selected as the current node
  • If one does not already exist, a new edge is added from the previous position to the current node
  • That edge has the current sequence label added to it; the number of labels on the edge correspond to the number of sequences that include that edge and those two nodes.

Fusing nodes whenever possible ensures that information about a motif that several times in several sequences in a similar location is not obscured by corresponding to several paths through the graph; It also increases the runtime of the algorithm by limiting the number of nodes and edges that need to be considered.

Note that one can always reconstruct any individual sequence inserted into the graph by looking up its starting point, and following edges labelled with the corresponding label through the graph.

Once an aligned sequence is inserted, a new topological sort of the nodes is generated, and another alignment can be perfomed.

Consensus paths

Now that you have all of your sequences in the graph, how do you get things like a consensus sequence out of it? This is the topic of a paper² separate from the first one.

Finding the single best-supported traversal through the graph is relatively straightforward. In fact, this is again a dynamic programming problem; one sets the scores of all nodes to zero, and then marches through the graph node by node. At each node, one chooses the “best” edge into that node – the one with the most sequences including it – and sets the score to be the edge weight plus the score of the node pointed to; and in case of a tie between edges, one chooses the one pointing to the highest-scoring node.

The highest score and the edges chosen gives you a maximum-weighted path through the graph. As is pointed out in the consensus paper, this is a maximum-likelihood path if the edge weights correspond to the probabilities that the edge is followed.

However, there may well be multiple consensus features in the alignment that one wishes to extract; a feature seen by multiple but still a minority of sequences. The approach to finding remaining consenses is necessarily somewhat heuristic, and comprises the bulk of the consensus paper.

The basic idea is to somehow remove or downweight the edges that correspond to the already-extracted consenses, and repeat the procedure to find additional features. The steps recommended in the consensus paper are:

• Identify sequences that correspond to the consensus just identified; by (eg) fraction of their bases/edges included, possibly with other requirements
• For edges corresponding to those sequences, reduce the weight corresponding to those sequences, possibly to zero
• Rerun the consensus algorithm.

In the simple implementation we use to demonstrate these ideas, we simply choose all (remaining) sequences that have a majority of their bases represented in the current consensus sequence, remove the corresponding weight of those edges entirely, and repeat until no further sequences remain or no significant consensus sequence is found.

The consensus paper identifies a particular corner case where a consensus sequence might terminate early; we allow this to happen.

Alignment strings

Finally, to communicate the alignment results, it can still be useful to generate a “flattened” alignment of the input and consensus sequences.

This is again fairly straightforwardly done once the graph is topologically sorted. Each node in the graph, in topological order, is assigned a column in the final table to be generated, with rings of nodes that are aligned to each other assigned to the same column, and nodes that are not aligned to any others getting their own column. Then the bases are filled in, with each sequence (including the consensus sequences) getting their own row.

Because we are assigning columns to the nodes in topologically-sorted order, the method used to generate the (non-unique) topological sort affects how the alignments look as alignment strings, even if they are all functionally identical. Kahn sorting tends to interleave the results of sequences, whereas depth-first-search necessarily visits long strings of runs in order. DFS then generates better looking alignment strings, so we use that approach in the implementation below.

Simple Implementation

A simple but fully functional Python implementation of the algorithms described above can be found here. For the alignment stage, two implementations are given; one that is quite simple to follow but is very slow; and another that is significantly faster, but may require a little more careful reading, as it uses numpy vectorization to improve performance.

Even the faster implementation is still slow – about 10 times slower than the poaV2 code written in C as distributed, or closer to 20 if poaV2 is compiled with -O3 – but is nonetheless useable for small problems.

The simple implementation above can generate HTML with an interactive graph visualization to explore the final partial order graph; the visualization works particularly well on browsers with a high-performance javascript implementation, but stops being useful for graphs with more than a thousand nodes or so.

Conclusion

Partial order alignment is a powerful technique that results in a graph containing rich information concerning the structure of the aligned sequences, but lacks the amount of online documentation and easy-to-explore implementations of some other methods; we hope this helps introduce a broader audience to a more in-depth understanding of the method.

---

References